1. Гармонійні коливання та їх характеристики
Коливальним називається процес багаторазового відхилення певної фізичної величини від її рівноважного стану й повернення до нього. Якщо це відбувається через однакові проміжки часу (тобто нескінченну кількість разів), коливання називаються періодичними, а ці проміжки часу – періодом коливання.
Коливання широко представлені у природі й у техніці. Незважаючи на їх різноманітну фізичну природу, всі вони мають деякі загальні закономірності й можуть бути зведені до суперпозиції найпростіших періодичних коливань, що називаються гармонійними
Поки ми обмежимося дослідженнями загальних закономірностей коливальних процесів і механічними коливними системами.
Для одержання гармонійного коливання розглянемо рівномірний рух по колу радіуса ![]() з центром у точці
з центром у точці ![]() кінця радіус-вектора
кінця радіус-вектора ![]() – точки
– точки ![]() (рис. 1), який відбувається нескінченно довго. Її стала кутова швидкість обертання
(рис. 1), який відбувається нескінченно довго. Її стала кутова швидкість обертання ![]() дорівнює частці від поділу кута повороту
дорівнює частці від поділу кута повороту ![]() вектора
вектора ![]() (щодо його початкового положення в нульовий момент часу
(щодо його початкового положення в нульовий момент часу ![]() вздовж осі
вздовж осі ![]() введеної декартової системи координат) на час повороту
введеної декартової системи координат) на час повороту ![]() :
: ![]() . Її називають також кутовою частотою обертання. Вона визначає період обороту
. Її називають також кутовою частотою обертання. Вона визначає період обороту ![]() й частоту обертання, яку традиційно позначають через
й частоту обертання, яку традиційно позначають через ![]() (грецька буква "ню"):
(грецька буква "ню"):
![]() ,
, ![]() .
.
![]() . (1)
. (1)
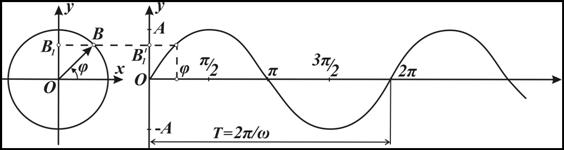
Рис. 1. Прийом розвертання гармонійних коливань у часі
Відомі із тригонометрії коливання величини ![]() (1) вздовж вертикальної осі біля нульового рівноважного положення з розмахом від
(1) вздовж вертикальної осі біля нульового рівноважного положення з розмахом від ![]() до
до ![]() з основним періодом
з основним періодом ![]() по змінній
по змінній ![]() (з періодом
(з періодом ![]() по змінній
по змінній ![]() ) називаються гармонійними. Для зручності аналізу їх "розвертають" у часі, відкладаючи аргумент – кут повороту
) називаються гармонійними. Для зручності аналізу їх "розвертають" у часі, відкладаючи аргумент – кут повороту ![]() (або пропорційний йому час
(або пропорційний йому час ![]() ) по горизонталі. При цьому коливання зображуються у прямокутній декартовій системі координат
) по горизонталі. При цьому коливання зображуються у прямокутній декартовій системі координат ![]() так званою синусоідою (див. рис. 1).
так званою синусоідою (див. рис. 1).
При описі гармонійних коливань уведені раніше для обертового руху величини ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (за винятком кута
(за винятком кута ![]() , усі вони є принципово позитивними) іменують вже трохи інакше:
, усі вони є принципово позитивними) іменують вже трохи інакше: ![]() – період коливання,
– період коливання, ![]() і
і ![]() – його частота й кругова частота, відповідно,
– його частота й кругова частота, відповідно, ![]() і
і ![]() – фаза й амплітуда коливання. Очевидно, що фаза коливання визначається з точністю до доданку, кратному
– фаза й амплітуда коливання. Очевидно, що фаза коливання визначається з точністю до доданку, кратному ![]() .
.
Узагальнюючи опис коливань (1), можна вважати, що в нульовий момент часу фаза коливання ![]() має якесь, у загальному випадку відмінне від нуля, значення
має якесь, у загальному випадку відмінне від нуля, значення ![]() – початкову фазу:
– початкову фазу:
![]() . (2)
. (2)
![]() , (3)
, (3)
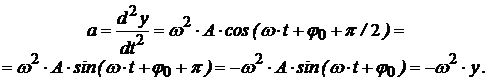 (4)
(4)
Звідси можна зробити такі висновки:
1. Швидкість (3) і прискорення (4) величини ![]() , що виконує гармонійні коливання, є також гармонійними коливаннями з тією же частотою
, що виконує гармонійні коливання, є також гармонійними коливаннями з тією же частотою ![]() .
.
2. Амплітуди й фази цих трьох гармонійних коливань (2) – (4) різні. При цьому коливання швидкості ![]() й прискорення
й прискорення ![]() випереджають по фазі основне коливання величини
випереджають по фазі основне коливання величини ![]() , відповідно, на
, відповідно, на ![]() (на чверть періоду) і на
(на чверть періоду) і на ![]() (на півперіоду, тобто, перебуває у протифазі).
(на півперіоду, тобто, перебуває у протифазі).
3. Величина ![]() , що виконує гармонійні коливання, пов'язана зі своїм прискоренням
, що виконує гармонійні коливання, пов'язана зі своїм прискоренням ![]() простим співвідношенням:
простим співвідношенням: ![]() , причому знак прискорення
, причому знак прискорення ![]() завжди протилежний знаку зсуву
завжди протилежний знаку зсуву ![]() , або:
, або:
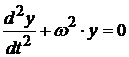 . (5)
. (5)
![]() .
.